之所以单开一个新的空间来存放像Z得分、标准误差、T分布这样的知识点，是因为在统计推断这个统计学的核心概念里，它们同时被参数估计与假设检验所需要

Z得分

Z得分是衡量数据点相对于其数据集平均值的偏离程度，用标准差的倍数表示。

Z得分的计算公式是：

$\begin{equation}\label{Z} Z = \frac{X - \mu}{\sigma} \end{equation}$

其中：

$Z$ 是Z得分。
$X$ 是观测值。
$\mu$ 是数据集的平均值。
$\sigma$ 是数据集的标准差。

通过这个公式，你可以将任何观测值转换成Z得分，这表示该观测值相对于整个数据集平均值的偏离程度，以标准差为单位。这个分数可以是正数、负数，或者零：

正数表示观测值高于平均值。
负数表示观测值低于平均值。
零表示观测值等于平均值。

标准误差

标准误差就像一把尺子，这把尺子每个总体都会拥有一把，专门为该总体定制。 > >当我们使用统计量来估计参数时，这把尺子的作用是度量在处理特定样本量时计算出的某个特定统计量——通常是样本均值——相对于总体参数，通常是总体均值，的准确度和可靠性。 > >这把尺子是非常独特的，因为它的刻度不是固定的，而是随着样本量的大小变化而变化。当样本量增加时，这把尺子的刻度会变得更加紧凑，意味着统计量与参数之间的差异变得更小，我们的估计也就更加接近真实的总体参数值。换句话说，随着我们增加样本量，这把尺子帮助我们更精确地测量统计量对总体参数的估计，从而减少估计的不确定性。另一方面，这把尺子也反映了总体内在的变异性。总体变异性越大，即总体标准差越大，这把尺子告诉我们即使是对同一个总体参数的估计也会有较大的波动。这就像是尺子的刻度在变宽，提示我们即便使用相同的样本量，不同样本之间的统计量也可能有较大的差异。总之，标准误差这把尺子是统计学家的宝贵工具。它不仅帮助我们量化使用样本数据估计总体参数时的准确度和可靠性，还教导我们关于样本量大小和总体变异性如何影响我们的估计。通过这把尺子，我们能够更加自信地进行统计推断，理解和解释我们从样本数据中得出的结论。 > >统计量相对于参数当用于衡量统计量围绕参数展开分布的离散程度的指标，更确切地说，它用来衡量样本均值作为总体均值估计的准确性

尺子的定义

这把尺子——标准误差（SE）的计算公式是基于总体标准差（$\sigma$）和样本大小（$n$）：

$ SE = $

其中：

$SE$ 是标准误差，代表样本均值的分布标准差，即我们讨论的“尺子”的精确度；
$\sigma$ 是总体标准差，代表总体数据点相对于总体均值的平均偏差，反映了总体内的变异性；
$n$ 是样本大小，即从总体中抽取用于分析的数据点数量。

尺子的应用场景

当总体标准差 ($\sigma$) 已知时，这个公式可以直接用来计算标准误差。然而，在实际研究中，我们往往不知道总体标准差，因此会使用样本标准差（$s$）来代替 $\sigma$，相应地，标准误差的计算公式变为：

$ SE = $

其中 $s$ 是样本标准差，它是基于抽取的样本计算得出的。

标准误差的意义

- 准确度的衡量：标准误差度量了样本均值作为总体均值估计的准确度。标准误差越小，表示我们的样本均值越接近总体均值，即我们的估计越准确。

- 样本量的影响：公式中的 $\sqrt{n}$ 显示了增加样本量如何减小标准误差，从而提高估计的准确度。这是因为较大的样本更能代表总体，减少了抽样误差。

这个“尺子”的计算公式不仅简单但极其强大，它是进行科学研究和数据分析时不可或缺的工具，帮助我们量化统计估计的准确度。

t

t分布

更公正地使用小样本来描述推断总体均值

t分布的发现

戈塞特对于t分布的发现，具体来说，是一个关于如何在只有少量样本数据时估计总体均值的统计问题的解决方案。他注意到，当样本量较小时，样本标准差与总体标准差之间存在较大的不确定性，这影响了基于正态分布的推断的准确性。t分布的发现背后的数学原理和思考过程可以分为以下几个关键步骤：

样本标准差的不确定性

在小样本情况下，样本标准差作为总体标准差的估计具有较高的不确定性。这意味着，使用样本标准差来标准化样本均值（从而计算z得分）会导致推断过程中的误差增大。

寻找适用于小样本的分布

戈塞特通过实验和数学推导寻找一个可以准确描述样本均值分布的概率分布，这个分布需要能够考虑到样本标准差的不确定性。他发现，当样本量较小时，样本均值的分布不再是正态分布，而是一种新的分布——现在被称为t分布。

t分布的特性

t分布的形状依赖于自由度（通常为样本大小减1）。对于较小的样本量，t分布比正态分布更加“扁平”（即，在均值附近的概率密度较低，尾部较重）。这意味着，在小样本情况下，t分布提供的置信区间比基于正态分布的置信区间要宽，更加保守，从而更好地反映了实际的不确定性。
随着样本量的增加，t分布逐渐接近正态分布。当样本量足够大时（例如，超过30），t分布和正态分布几乎没有区别，这时可以使用正态分布的方法来进行估计和推断。

数学表达

t分布的数学公式表达了戈塞特的这一发现。给定一个样本均值$\bar{x}$，总体均值$\mu$，样本标准差$s$，和样本大小$n$，t值定义为：

$\begin{equation}\label{t} t = \frac{\bar{x} - \mu}{s/\sqrt{n}} \end{equation}$

这个t值随后被用来从t分布表中查找p值或者置信区间，这种方式考虑了样本标准差的不确定性和样本大小。

戈塞特的工作是统计学和实际应用研究的一个重要里程碑，它为小样本数据分析提供了一个强大的工具，至今仍被广泛应用于各个领域。

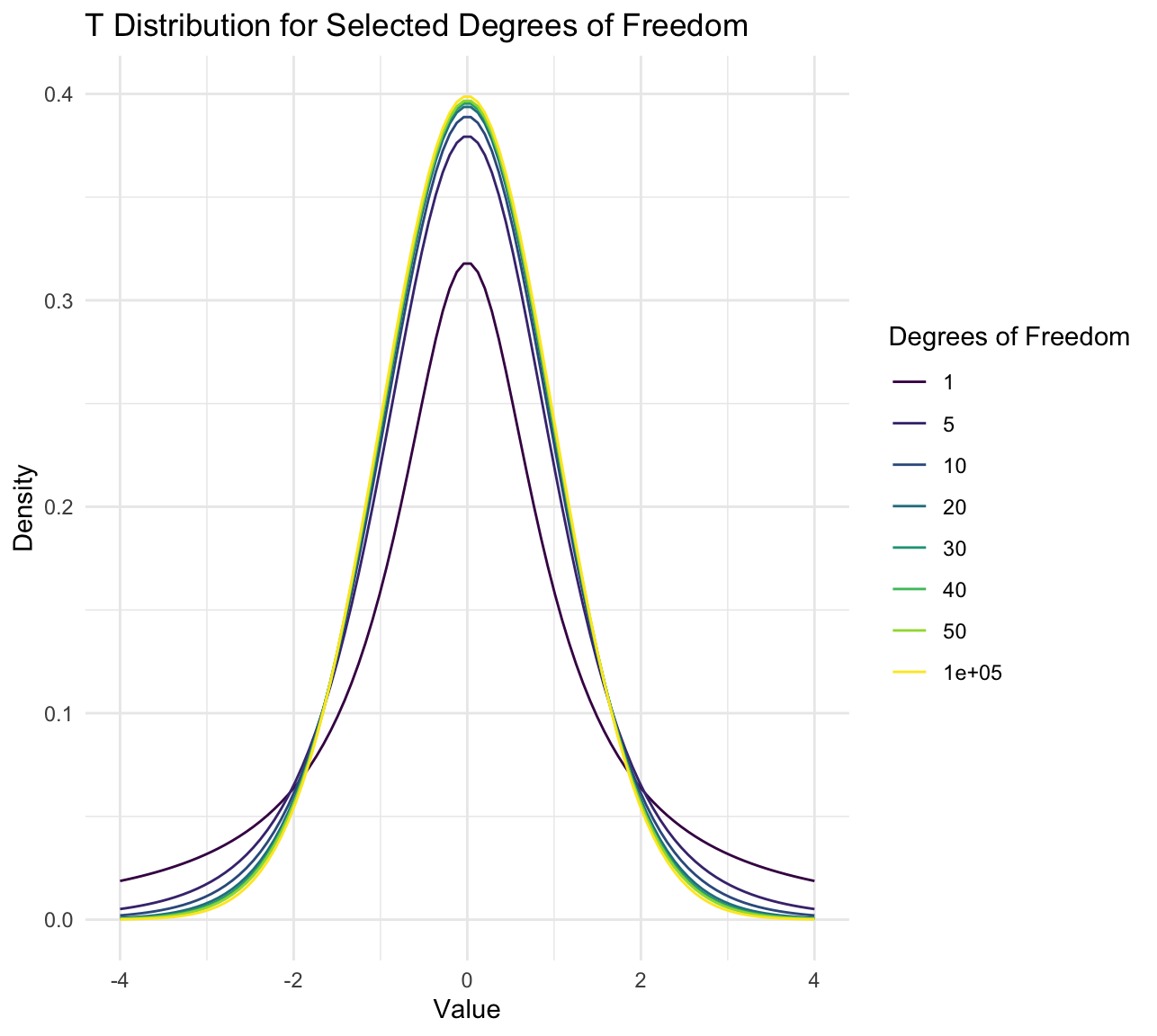
t分布根据自由度的不同展开为分布簇，每个自由度下的t分布的图形都不一样，有趣的是，自由度越大，t分布的图像就越接近正态分布，可以尝试使用R语言来绘制t分布的图像，代码如下、结果如下

# 载入ggplot2包进行绘图
library(ggplot2)

# 选择展示的自由度值
dfs <- c(1, 5, 10, 20, 30, 40, 50, 100000)

# 创建一个空的数据框来存储t分布数据
df_t_selected <- data.frame(x = numeric(), density = numeric(), df = integer())

# 生成选定自由度的t分布数据
for(df in dfs) {
  x <- seq(-4, 4, length.out = 100) # 生成值序列
  density <- dt(x, df) # 计算密度
  df_t_selected <- rbind(df_t_selected, data.frame(x, density, df = as.factor(df))) # 添加到数据框
}

# 使用ggplot2绘图
ggplot(df_t_selected, aes(x = x, y = density, color = df)) +
  geom_line() + # 绘制线条
  labs(title = "T Distribution for Selected Degrees of Freedom",
       x = "Value",
       y = "Density",
       color = "Degrees of Freedom") +
  theme_minimal() +
  scale_color_viridis_d() # 使用viridis颜色方案增强可视化

应用

哲の博客

统计推断的工具池

Z得分