引入
问题0
正态分布分布是什么?它是怎么来的?
中心极限定理
结论:一组随机变量满足独立且同分布,且这个共同的分布具有有限的均值和方差,那么无论这些随机变量本身服从何种分布,当随机变量的数量足够多时(通常认为n>30定理成立,但并不绝对),这些随机变量的和(或它们的平均值)的分布将趋向于正态分布
正态分布是中心极限定理的发展
中心极限定理是什么?
例1:
假设你有100万人身高的数据,你定义样本X,样本大小为50,命令1000人每人制作一个样本X,当你收取1000人的样本均数\(X_n\)时,定义变量为\(X_n\),绘制\(X_n\)的频数分布直方图,你会得到一个钟形曲线,也叫高斯曲线
进化
假设你从赌场获得了一批偏心骰子,这个骰子掷出1的概率为50%,掷出2、3、4、5、6的概率都为10%,投掷10次为1组,记录下每次的结果,你命令1000人每人产生一组结果同时计算骰子10次投掷结果的算数均数,把这个算数均数为\(C_n\),定义变量\(C_n\),绘制变量\(C_n\)的频率分布直方图
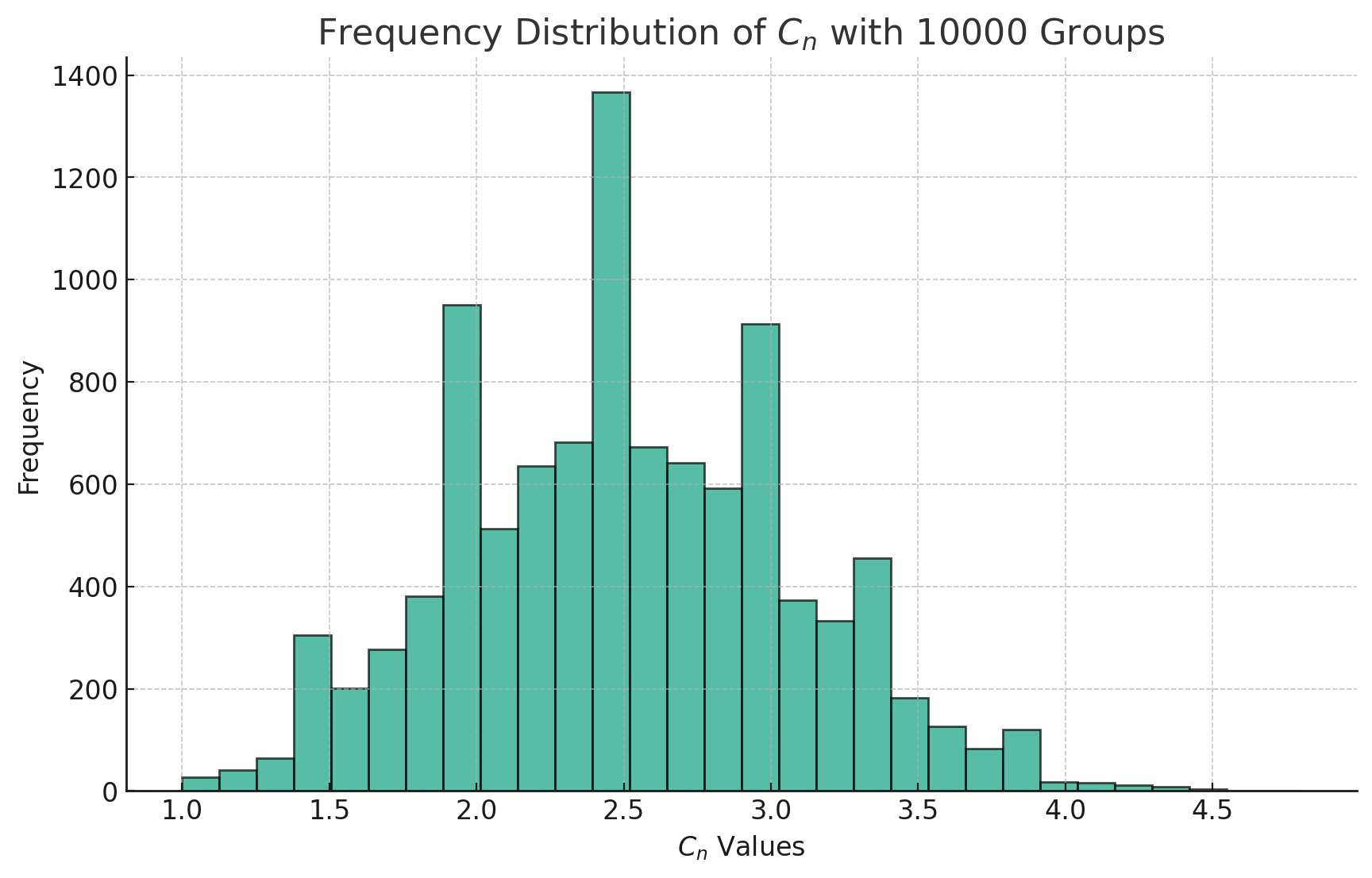
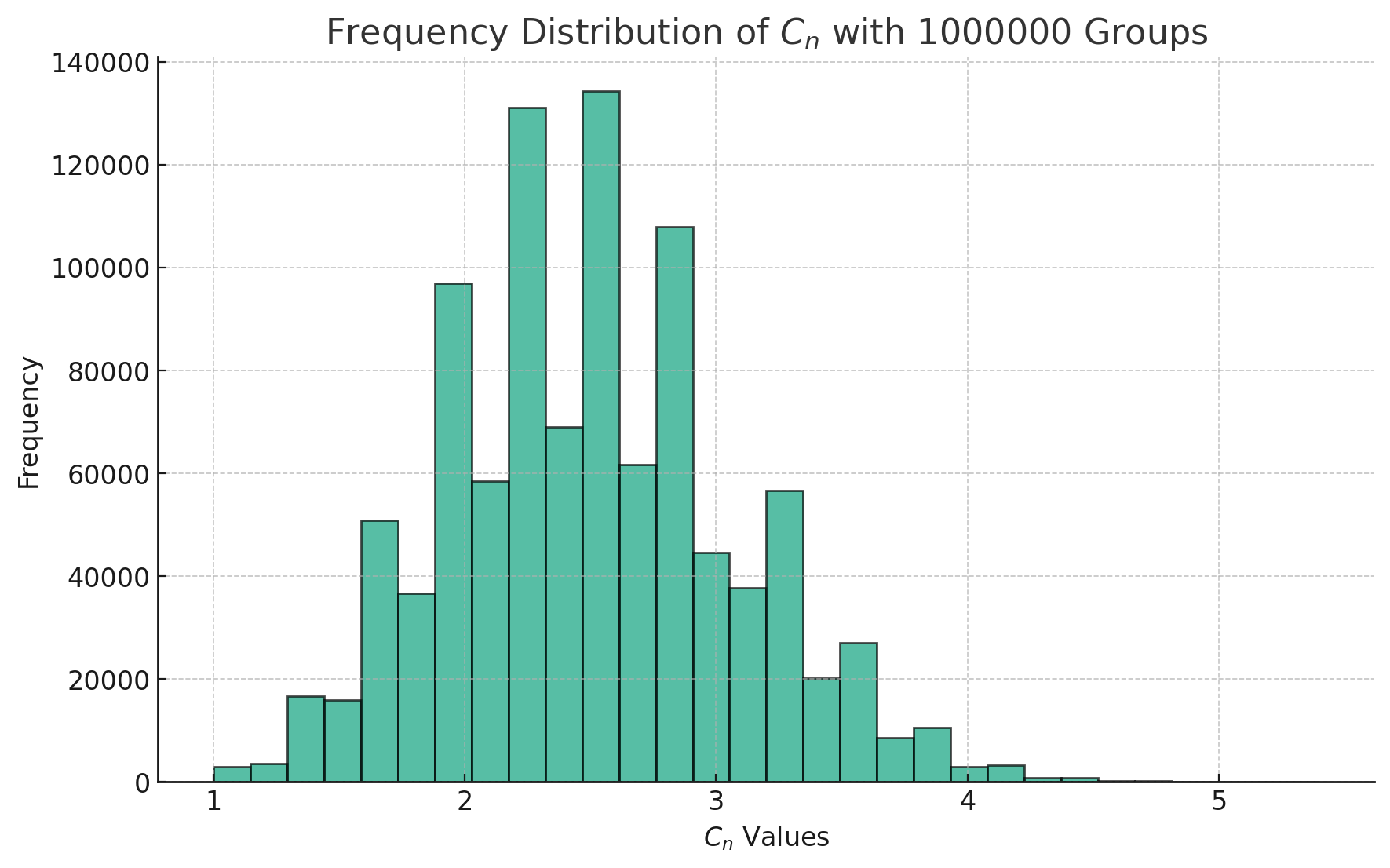
目前我的能力限制我无法理解公式的来源,先记住它:
完成上述步骤后,高斯得到了正态分布的密度函数的标准形式:
$ f(x) = e^{-} $
在这里,\(\mu\) 是误差的平均值,\(\sigma^2\) 是方差,它们分别代表了测量误差的中心位置和分布的宽度。
正态分布的3σ(3西格玛)法则,也称为经验法则,是基于正态分布性质的一个规则,它描述了数据点分布在其平均值周围的情况。这个法则是从正态分布的数学性质中直接推导出来的。
正态分布的定义
首先,回顾一下正态分布的数学定义:一个随机变量 \(X\) 如果服从一个均值为 \(\mu\),标准差为 \(\sigma\) 的正态分布,其概率密度函数(PDF)为:
$ f(x) = e^{-} $
3σ法则的来源
正态分布的一个关键特性是其对称性和特定的概率分布形状。3σ法则利用了正态分布的这些性质,具体规则如下:
- 约68.27%的数据点落在 \(\mu - \sigma\) 和 \(\mu + \sigma\) 之间(即平均值一个标准差内)。
- 约95.45%的数据点落在 \(\mu - 2\sigma\) 和 \(\mu + 2\sigma\) 之间(即平均值两个标准差内)。
- 约99.73%的数据点落在 \(\mu - 3\sigma\) 和 \(\mu + 3\sigma\) 之间(即平均值三个标准差内)。
数学推导
3σ法则的数学基础来自于正态分布的积分性质。具体地说,对正态分布的概率密度函数在特定区间内积分,可以得到数据点落在这个区间内的概率。例如,计算随机变量 \(X\) 的值落在 \(\mu - \sigma\) 和 \(\mu + \sigma\) 之间的概率,可以通过下面的积分得到:
$ P(- X + ) = _{- }^{+ } e^{-} dx $
通过对正态分布进行积分,我们可以得到上述的概率值。实际上,这些具体的概率值(68.27%,95.45%,99.73%)来自于正态分布的累积分布函数(CDF),它提供了随机变量取值小于或等于某个值的概率。
但数据的量化需要一个标准,于是标引入准分布,定义变量Z
\(Z = \frac{X - \mu}{\sigma}\)
绘制变量Z的频率直方图,得到标注的正态分布的曲线
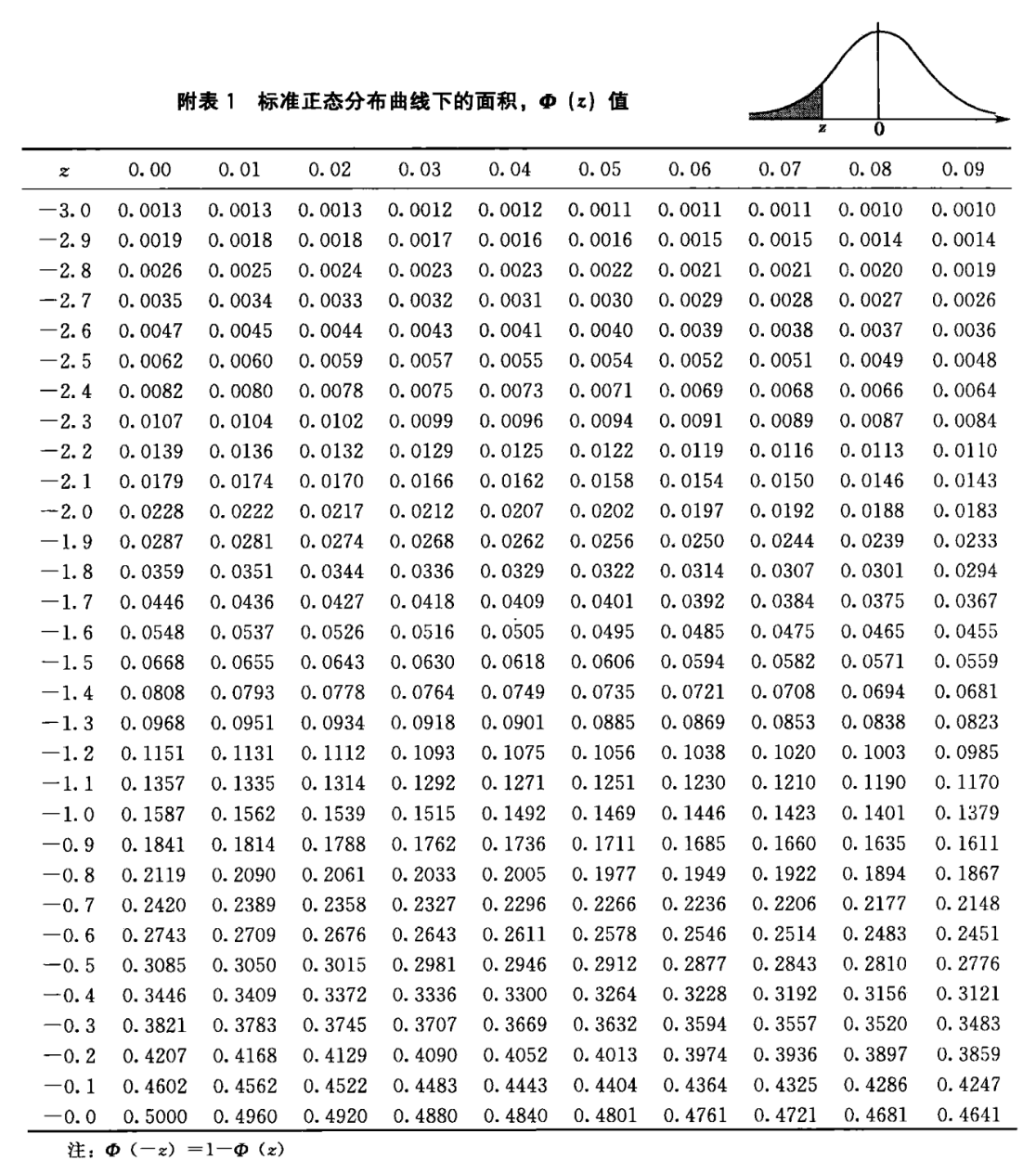
Z值表如下(也叫\(\phi或\Phi\),读作fai)
正态分布的性质
- 均值:
\(\mu_Z = \mu_X + \mu_Y\)
\(\mu_W = \mu_X - \mu_Y\)
- 方差:
\(\sigma_W^2 = \sigma_X^2 + \sigma_Y^2\)
为什么正态分布中方差只加不减
方差的性质 \(\sigma_W^2 = \sigma_X^2 + \sigma_Y^2\),当考虑两个随机变量 \(X\) 和 \(Y\) 的差 \(W = X - Y\) 时,即使是在它们的差的情况下,方差之和而不是方差之差出现在公式中,这背后的原因与随机变量的独立性和方差的数学性质有关。
独立性
当两个随机变量 \(X\) 和 \(Y\) 独立时,它们之间没有相互影响。这意味着一个变量的变化不会影响另一个变量的分布。因此,当我们计算它们的和或差的方差时,我们只需要考虑每个变量自身的变异性,而不是它们之间的相互作用。
方差的定义
方差衡量随机变量和其均值的偏差的平方的平均值,是衡量随机变量分散程度的度量。方差的计算公式为 \(\sigma^2 = E[(X - \mu)^2]\),其中 \(E\) 表示期望值操作符,\(\mu\) 是随机变量 \(X\) 的均值。
方差的加法性质
对于独立随机变量的和或差,方差的加法性质说明,总的方差是各个随机变量方差的和。数学上,这可以通过方差的定义和随机变量的独立性质推导得出。对于差 \(W = X - Y\),其方差为:
\[\begin{align*} \sigma_W^2 &= \text{Var}(X - Y) \\ &= \text{Var}(X) + \text{Var}(-Y) \\ &= \sigma_X^2 + \text{Var}(-Y) \end{align*}\]
由于 \(\text{Var}(aY) = a^2\text{Var}(Y)\)(这里 \(a = -1\)),我们有:
\[\begin{align*} \text{Var}(-Y) &= (-1)^2\text{Var}(Y) \\ &= \text{Var}(Y) \\ &= \sigma_Y^2 \end{align*}\]
因此,
\(\sigma_W^2 = \sigma_X^2 + \sigma_Y^2\)
这显示了,即使是随机变量的差,其方差也是组成随机变量方差的总和。这是因为方差衡量的是变异性,而变异性在随机变量相加或相减时是累积的,不考虑方向(正或负)。为什么正态分布中均值有加有减
这是因为随机变量的期望值(均值)具有线性性质。具体来说,随机变量的期望值(或均值)遵循以下规则:
假设 \(X\) 和 \(Y\) 是两个随机变量,且 \(\mu_X\) 和 \(\mu_Y\) 分别是它们的期望值(均值)。如果我们定义一个新的随机变量 \(W = X - Y\),那么 \(W\) 的期望值(均值)是 \(X\) 和 \(Y\) 均值的差,即:
\(E[W] = E[X - Y]\)
根据期望值的线性性质,我们有:
\(E[X - Y] = E[X] - E[Y]\)
这就是说:
\(\mu_W = \mu_X - \mu_Y\)
原因解释:
期望值的线性性质:这个性质说明,任意两个随机变量 \(X\) 和 \(Y\) 的线性组合的期望值等于各自期望值的相同线性组合。简单来说,就是你可以将期望值的运算“分发”到随机变量的运算中。
独立与非独立随机变量:值得注意的是,这个性质不依赖于 \(X\) 和 \(Y\) 是否独立。无论 \(X\) 和 \(Y\) 之间的关系如何,\(W = X - Y\) 的期望值都是 \(\mu_X - \mu_Y\)。