极限
极限描述的仅仅是一个函数趋近于某个点的行为—可汗学院-微分
极限值与那个点没有任何关系
极限的估算办法
- 使用图像
- 使用表格
- 计算两个方向临近某点的值
极限的定义
微分学中的极限定义是数学分析中非常基础且关键的概念。极限的定义有多种形式,其中最经典的是ε-δ(epsilon-delta)定义,用于确立函数在某点的极限。以下是其基本形式:
函数在点的极限定义(ε-δ定义)
设函数 \(f(x)\) 在点 \(a\) 的一个去心邻域内有定义。若对于任意给定的正数 \(\epsilon\)(无论它多么小),总存在一个正数 \(\delta\),使得当 \(x\) 满足 \(0 < |x - a| < \delta\) 时,有 \(|f(x) - L| < \epsilon\),则称数 \(L\) 是 \(f(x)\) 当 \(x\) 趋向于 \(a\) 时的极限,记为
\(\lim_{x \to a} f(x) = L\)

直观理解
ε-δ 定义的本质是无论我们希望 \(f(x)\) 的值和其极限 \(L\) 之间的差距多么小(即 \(|f(x) - L| < \epsilon\)),我们总能找到一个足够小的区间 \((a-\delta, a+\delta)\)(去掉点 \(a\)),使 \(x\) 在这个区间内时,\(f(x)\) 与 \(L\) 的差距确实如我们所希望的那样小。
数列的极限定义则强调了,随着数列的项数增加,数列的项越来越接近某个值 \(L\),并且可以任意接近,只要项数足够大。
这些定义虽然在形式上看起来比较抽象,但它们为微分学和整个数学分析的发展提供了坚实的基础。通过这些精确的定义,数学家能够严格地讨论函数和数列的性质,以及它们随着输入变化或项数增加时的行为。
极限的性质
- 加
- 减
- 乘
- 除
- 若\(\frac 1 0\),那么极限不存在
- 若\(\frac 0 0\),那么要想办法继续分析
- 指数性质
极限的计算
法则:
极限的计算法则和导数的计算法则虽然相关,但它们并不完全相同。这两个概念在微积分中都非常基础,但用途和计算方法有所不同。下面简要概述它们的主要区别和联系:
极限的计算法则
极限的计算法则主要关注于当变量接近某个值时,函数的行为。一些基本的极限计算法则包括:
- 和法则:\(\lim_{x \to a} (f(x) + g(x)) = \lim_{x \to a} f(x) + \lim_{x \to a} g(x)\)
- 乘积法则:\(\lim_{x \to a} (f(x) \cdot g(x)) = (\lim_{x \to a} f(x)) \cdot (\lim_{x \to a} g(x))\)
- 商法则:\(\lim_{x \to a} \frac{f(x)}{g(x)} = \frac{\lim_{x \to a} f(x)}{\lim_{x \to a} g(x)}\),前提是\(\lim_{x \to a} g(x) \neq 0\)
- 复合函数极限法则:如果\(\lim_{x \to a} g(x) = b\),且\(\lim_{y \to b} f(y)\)存在,则\(\lim_{x \to a} f(g(x)) = \lim_{y \to b} f(y)\)
导数的计算法则
导数的计算法则关注的是函数在某一点的瞬时变化率。导数的一些基本计算法则包括:
- 和法则:\((f(x) + g(x))' = f'(x) + g'(x)\)
- 乘积法则:\((f(x) \cdot g(x))' = f'(x) \cdot g(x) + f(x) \cdot g'(x)\)
- 商法则:\(\left(\frac{f(x)}{g(x)}\right)' = \frac{f'(x) \cdot g(x) - f(x) \cdot g'(x)}{(g(x))^2}\)
- 链式法则:如果\(y = f(u)\)且\(u = g(x)\),则\(\frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx}\)
相关与区别
- 相关性:导数的定义本身就基于极限的概念,即导数可以被定义为一个极限。例如,函数\(f(x)\)在点\(x=a\)的导数定义为\(\lim_{h \to 0} \frac{f(a+h) - f(a)}{h}\)。
- 区别:尽管导数的定义依赖于极限,但计算导数的法则专门针对函数的瞬时变化率,而计算极限的法则更广泛,涵盖了函数值随变量变化趋向某一值的行为。
简而言之,虽然导数和极限都是微积分中的核心概念,它们的计算法则旨在解决不同类型的问题,但导数的计算是建立在极限概念之上的。
- 需先计算复合函数正负极限,用这两个数字一起确定复合函数是否存在极限
- 连续的函数可以直接代入求极限
代数求极限
我认为,代数求极限的本质是将函数a转化为函数b,因为函数a转化为函数b时,函数a上的某些没有意义的点在函数b突然有了定义,而且还连续
- 因式分解
- 有理化
- 进行有理化前注意函数的定义域
- 有理化的目的是避免走\(\frac 0 0\)
- 用恒等式求三角函数极限
- \({\cos x}^2+{\sin x}^2 = 1\)
- \(\cos 2x ={cos x}^2-{sin x}^2=1-2{sin x}^2=2{cos x}^2-1\)
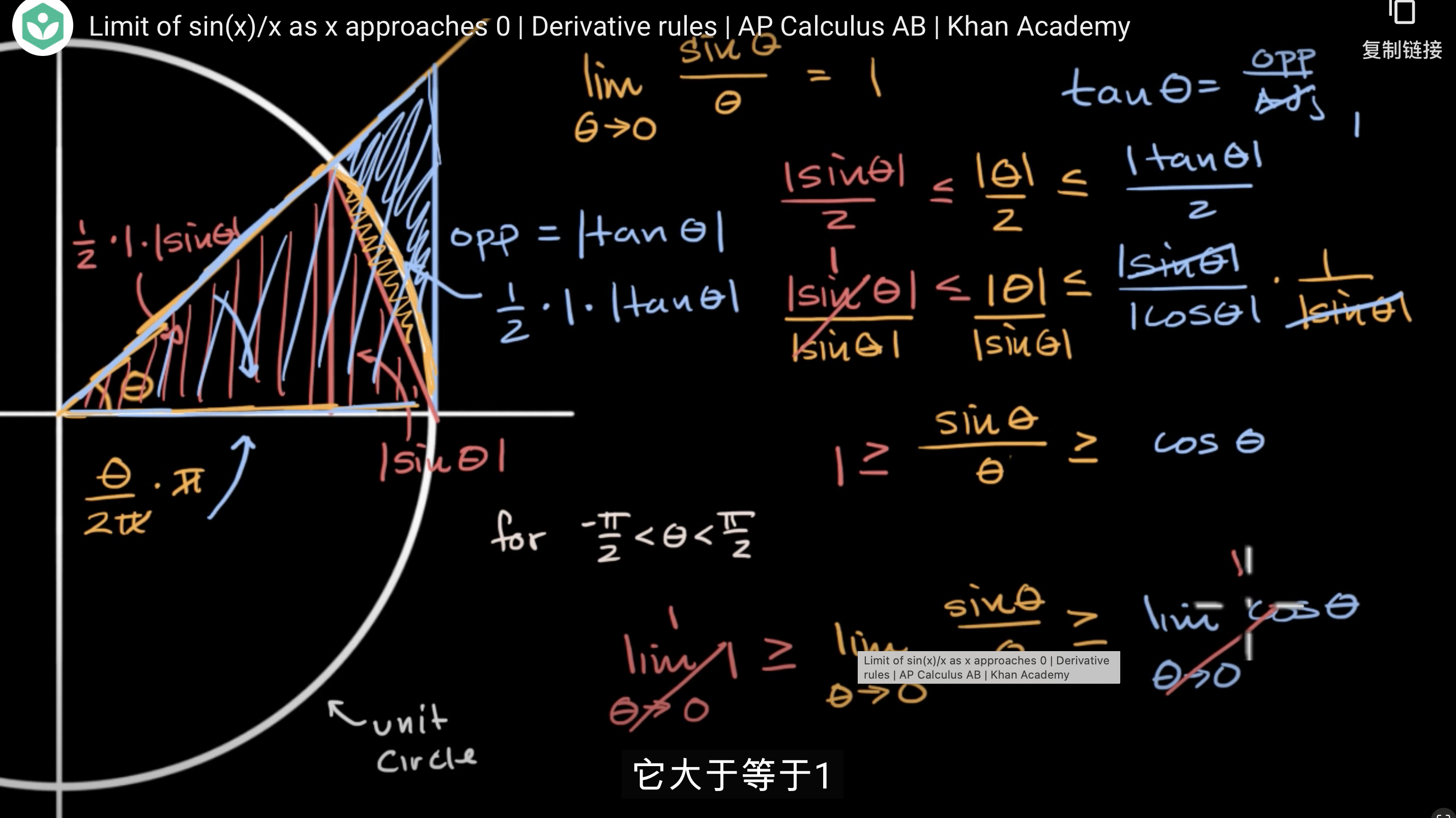
夹逼定理求极限
- \({lim}_{x\rightarrow0}\frac{\sin{x}}{x}=1\)
- \(\operatorname*{lim}_{x\rightarrow0}\frac{1-\cos{x}}{x}=1\)

无穷大的极限
- 商的极限


中值定理
对于函数y,在闭合的区间[a,b]内连续,若有c在区间[a,b]内,那么一定存在\(y(c)在y(a)与y(b)之间\)
导数
切线:瞬时变化率
割线:平均变化率
定义
导数是微积分学中的一个基本概念,用于衡量一个函数在某一点处的变化率。给定一个实值函数\(f(x)\)和一个属于该函数定义域的点\(a\),\(f(x)\)在点\(a\)处的导数(如果存在)是当\(x\)趋向于\(a\)时,函数增量\(f(x) - f(a)\)与自变量增量\(x - a\)的比值的极限。用数学语言描述,\(f(x)\)在点\(a\)处的导数定义为:
$ f'(a) = _{x a} $
如果这个极限存在,则称函数\(f(x)\)在点\(a\)处可导,并且这个极限值称为\(f(x)\)在点\(a\)处的导数。这个定义也称为函数在某一点的瞬时变化率或斜率。
导数有多种表示方式,如\(f'(x)\),\(\frac{df}{dx}\),或者\(\frac{d}{dx}f(x)\),都用来表示函数\(f(x)\)的导数。
导数的概念可以扩展到高阶导数,即导数的导数。第二导数、第三导数等分别表示函数曲线的凹凸性、变化率的变化率等属性。
导数在物理学、工程学、经济学等多个领域内都有广泛的应用,如表示速度、加速度、力的变化等。
导数可以利用极限的定义计算出来
函数可导,那么函数连续
垂直不能微分,不连续不能微分
导数的计算
幂法则
- \(\frac d{dx}[x^n]=n\cdot x^{n-1}\)
- 多项式求导
- \(\frac d{dx}[x^n]=n\cdot x^{n-1}\)
\(\frac d{dx}[lnx]=\frac 1 x\)
\(\frac d{dx}[e^x]=e^x\)
\(\frac d{dx}[cosx]=sinx\)
指数函数求导
把指数函数转化为\(e^x\)的形式进行求导
对数函数求导
因为lnx导数为1/x,所以将所有的对数函数转化为包含lnx
\(log_a^x=\frac{log_c^x}{log_c^x}\)
导数的性质
导数的乘法性质主要体现在两个重要的规则上:乘积规则和商法规则。这些规则使我们能够计算两个函数乘积或商的导数。
- 乘积规则
假设有两个可导函数\(f(x)\)和\(g(x)\),则它们乘积的导数可以用下面的公式来表示:
$ (f(x) g(x))' = f'(x) g(x) + f(x) g'(x) $
这个规则告诉我们,一个函数乘积的导数等于第一个函数的导数乘以第二个函数,加上第一个函数乘以第二个函数的导数。
- 商法规则
同样,如果有两个可导函数\(f(x)\)和\(g(x)\),并且\(g(x)\)不为零,则它们的商的导数可以用以下公式表示:
$ ( )' = $
这个规则表明,函数的商的导数等于分子的导数乘以分母,减去分子乘以分母的导数,整个表达式再除以分母的平方。
这两个乘法性质是解决微积分问题时的强大工具,特别是在需要找到复合函数导数时。通过应用这些规则,我们可以处理更复杂的函数,包括那些涉及乘法和除法运算的函数。
链式法则
复合函数可以写为\(w(u(x))\)
\(\frac d{dx}w(u(x))=w'(u(x))u'(x)\)